Dimensionality reduction techniques like PCA work wonderfully when datasets are linearly separable—but they break down the moment nonlinear patterns appear. That’s exactly what happens with datasets such as two moons: PCA flattens the structure and mixes the classes together. 

Kernel PCA fixes this limitation by mapping the data into a higher-dimensional feature space where nonlinear patterns become linearly separable. In this article, we’ll walk through how Kernel PCA works and use a simple example to visually compare PCA vs. Kernel PCA, showing how a nonlinear dataset that PCA fails to separate becomes perfectly separable after applying Kernel PCA.

What is PCA and how is it different from Kernel PCA?

Principal Component Analysis (PCA) is a linear dimensionality-reduction technique that identifies the directions (principal components) along which the data varies the most. It works by computing orthogonal linear combinations of the original features and projecting the dataset onto the directions of maximum variance. 

These components are uncorrelated and ordered so that the first few capture most of the information in the data. PCA is powerful, but it comes with one important limitation: it can only uncover linear relationships in the data. When applied to nonlinear datasets—like the “two moons” example—it often fails to separate the underlying structure.

Kernel PCA extends PCA to handle nonlinear relationships. Instead of directly applying PCA in the original feature space, Kernel PCA first uses a kernel function (such as RBF, polynomial, or sigmoid) to implicitly project the data into a higher-dimensional feature space where the nonlinear structure becomes linearly separable. 

PCA is then performed in this transformed space using a kernel matrix, without explicitly computing the higher-dimensional projection. This “kernel trick” allows Kernel PCA to capture complex patterns that standard PCA cannot.

We will now create a dataset that is nonlinear and then apply PCA to the dataset.

Code Implementation

Generating the dataset

We generate a nonlinear “two moons” dataset using make_moons, which is ideal for demonstrating why PCA fails and Kernel PCA succeeds.

import matplotlib.pyplot as plt
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=1000, noise=0.02, random_state=123)

plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()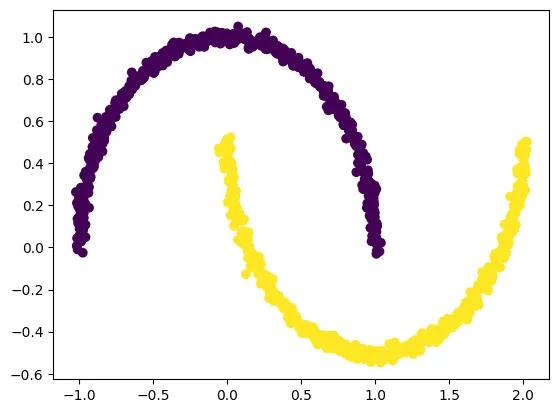

Applying PCA on the dataset

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

plt.title("PCA")
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)
plt.xlabel("Component 1")
plt.ylabel("Component 2")
plt.show()

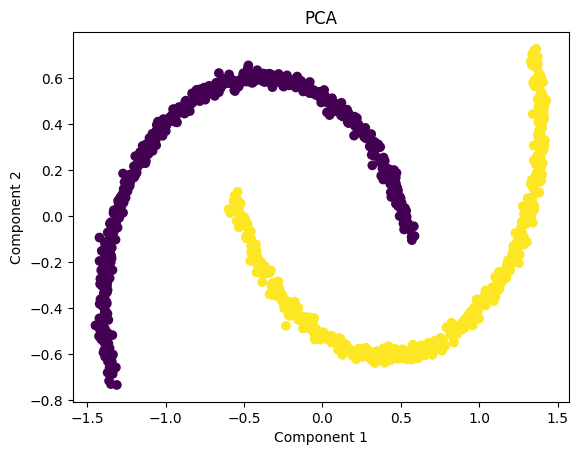
The PCA visualization shows that the two moon-shaped clusters remain intertwined even after dimensionality reduction. This happens because PCA is a strictly linear technique—it can only rotate, scale, or flatten the data along straight directions of maximum variance. 

Since the “two moons” dataset has a nonlinear structure, PCA is unable to separate the classes or untangle the curved shapes. As a result, the transformed data still looks almost identical to the original pattern, and the two classes remain overlapped in the projected space.

Applying Kernel PCA on the dataset

We now apply Kernel PCA using an RBF kernel, which maps the nonlinear data into a higher-dimensional space where it becomes linearly separable. In the kernel space the two classes in our dataset are linearly separable. Kernel PCA uses a kernel function to project the dataset into a higher-dimensional space, where it is linearly separable.

from sklearn.decomposition import KernelPCA
kpca = KernelPCA(kernel='rbf', gamma=15)
X_kpca = kpca.fit_transform(X)

plt.title("Kernel PCA")
plt.scatter(X_kpca[:, 0], X_kpca[:, 1], c=y)
plt.show()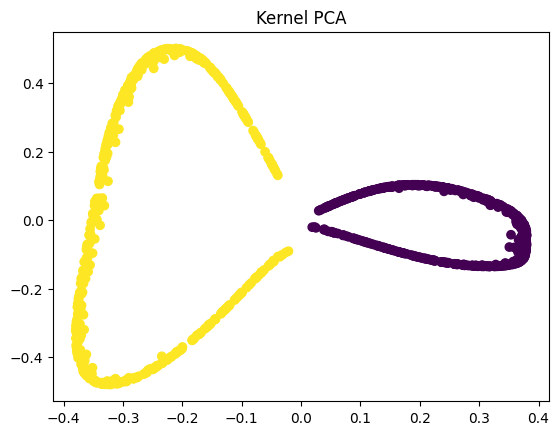

The goal of PCA (and dimensionality reduction in general) is not just to compress the data—it’s to reveal the underlying structure in a way that preserves meaningful variation. In nonlinear datasets like the two-moons example, traditional PCA cannot “unfold” the curved shapes because it only applies linear transformations.

Kernel PCA, however, performs a nonlinear mapping before applying PCA, allowing the algorithm to untangle the moons into two clearly separated clusters. This separation is valuable because it makes downstream tasks like visualization, clustering, and even classification far more effective. When the data becomes linearly separable after transformation, simple models—such as linear classifiers—can successfully distinguish between the classes, something that would be impossible in the original or PCA-transformed space.

Challenges involved with Kernel PCA

While Kernel PCA is powerful for handling nonlinear datasets, it comes with several practical challenges. The biggest drawback is computational cost—because it relies on computing pairwise similarities between all data points, the algorithm has O(n²) time and memory complexity, making it slow and memory-heavy for large datasets. 

Another challenge is model selection: choosing the right kernel (RBF, polynomial, etc.) and tuning parameters like gamma can be tricky and often requires experimentation or domain expertise. 

Kernel PCA can also be harder to interpret, since the transformed components no longer correspond to intuitive directions in the original feature space. Finally, it is sensitive to missing values and outliers, which can distort the kernel matrix and degrade performance.

Check out the FULL CODES here. Feel free to check out our GitHub Page for Tutorials, Codes and Notebooks. Also, feel free to follow us on Twitter and don’t forget to join our 100k+ ML SubReddit and Subscribe to our Newsletter. Wait! are you on telegram? now you can join us on telegram as well.

The post Kernel Principal Component Analysis (PCA): Explained with an Example appeared first on MarkTechPost.